La résolution de problèmes mathématiques au cours moyen

Pour résoudre des problèmes, les enfants comme les adultes s’appuient en priorité sur leur mémoire de problèmes résolus. L’enseignement de la résolution de problèmes a donc pour objectif d’engager les élèves dans la résolution d’une grande diversité de problèmes et de leur donner les moyens de repérer, parmi les problèmes résolus antérieurement, ceux susceptibles de les aider dans la résolution de nouveaux problèmes.

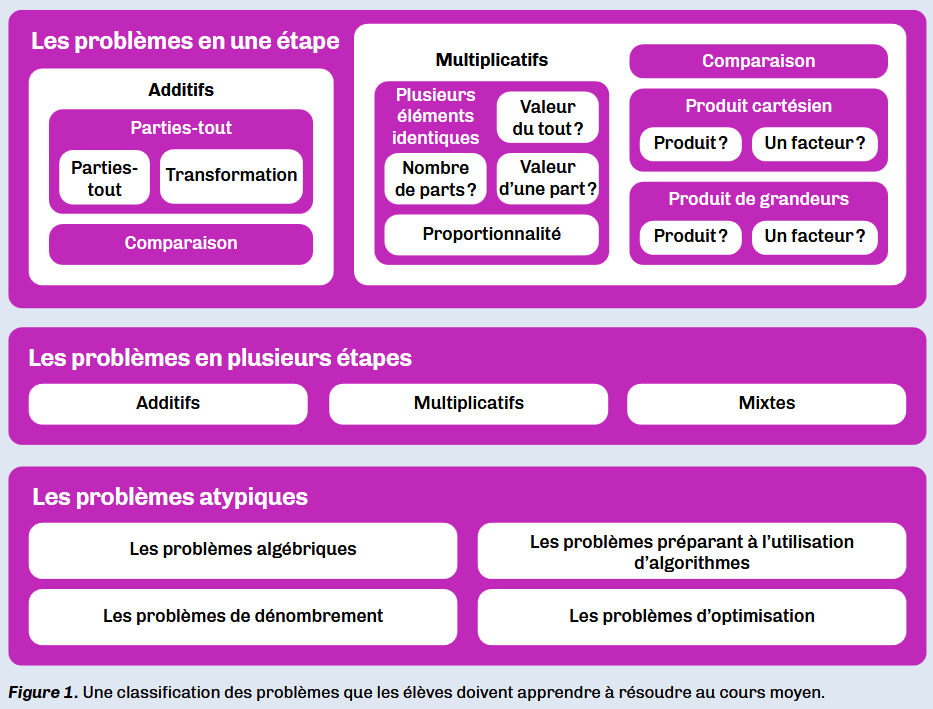
Classer les problèmes n’est pas un objectif d’enseignement et n’est pas une tâche dévolue aux élèves. Une classification des problèmes permet au professeur de structurer son enseignement, afin de s’assurer que les problèmes traités couvrent l’ensemble du spectre des problèmes devant pouvoir être résolus par des élèves de cours moyen.

Au cours moyen, le traitement de certains problèmes est quasi automatisé. Pour d’autres problèmes, en particulier une bonne partie des problèmes en plusieurs étapes et les problèmes atypiques, le traitement peut faire appel à une combinaison de stratégies utilisées dans divers problèmes avec une adaptation à la situation précise du problème.

La résolution d’un problème peut être vue comme un processus en quatre phases, qui ne se succèdent pas de manière stricte, mais qui sont en interaction permanente.
Comprendre : l’élève doit comprendre le texte du problème, c’est-à-dire comprendre l’histoire que raconte le problème. À cela s’ajoute une compréhension spécifique aux problèmes mathématiques : comprendre la question, identifier précisément ce qui est cherché.
Modéliser : l’élève doit traduire la situation comprise, l’histoire qui se situe dans le monde réel, dans un format pertinent sur le plan mathématique, par exemple un tout composé de parties, permettant de déduire des opérations mathématiques à effectuer pour répondre à la question posée.
Calculer : l’élève doit effectuer les calculs identifiés à l’étape précédente. Ces calculs peuvent être effectués mentalement, en ligne ou en posant les opérations.
Répondre : l’élève doit interpréter les résultats des opérations mathématiques dans le contexte du problème, en effectuant une régulation par rapport à la situation initialement comprise. Cette étape nécessite de mobiliser des compétences en communication pour produire une réponse intelligible par tous.

Trois sources principales de difficultés sont à retenir :
— la structure du problème.
Les problèmes en une étape sont d’une difficulté très hétérogène (voir chapitre 1). Les problèmes en plusieurs étapes, qui sont l’objectif principal de l’enseignement de la résolution de problèmes au cours moyen, sont en général plus difficiles que ceux en une étape. Les problèmes atypiques sont les moins connus des élèves et généralement les plus difficiles à résoudre.
— le texte de l’énoncé du problème.
Un énoncé de quelques lignes, éventuellement accompagné d’une illustration, peut poser de multiples difficultés de compréhension liées au contexte de l’énoncé, au lexique utilisé, aux représentations que se font les élèves en lisant l’énoncé, etc.
— les nombres en jeu.
Au cours moyen, les élèves rencontrent de nouveaux nombres (grands nombres, fractions, nombres décimaux) avec lesquels ils apprennent à calculer. Leur présence et des écritures de natures différentes dans les problèmes peuvent être sources de difficultés pour de nombreux élèves.

Pour construire des séquences et des séances d’enseignement de la résolution de problèmes, le professeur prend en compte ces trois sources de difficultés pour organiser :
— la progressivité des apprentissages des élèves ;
— la différenciation des tâches proposées ;
— l’accompagnement des élèves en difficulté.

Les apprentissages relatifs à la résolution de problèmes ne se construisent pas en une année ni même en un cycle, mais tout au long de la scolarité obligatoire. Les stratégies d’enseignement mises en œuvre doivent donc être collectives afin que les élèves puissent s’appuyer chaque année sur ce qui a été appris les années précédentes. Ceci est particulièrement vrai pour les schémas enseignés pour soutenir
la modélisation.

Les séances d’enseignement de résolution de problèmes doivent être inscrites dans des séquences aux objectifs clairement définis et explicités aux élèves. Pendant ces séances, les élèves doivent disposer de temps suffisants pour résoudre eux-mêmes les problèmes qui leur sont proposés. Il faut veiller à soutenir, de façon appropriée et au moment opportun, chaque élève rencontrant une difficulté qu’il ne
peut pas surmonter lui-même.

L’évaluation doit être utilisée pour soutenir les apprentissages. Elle permet à l’enseignant de renforcer sa connaissance de ce que sait faire chacun des élèves à un instant donné et aide les élèves à structurer et renforcer leurs apprentissages comme le montrent les sciences cognitives.